If You Had To Point Out The Flaws Of The Stock Market Relative To Other Asset Classes What Would They Be?
There’s a long list of them, high volatility, sequence of return risk, low cashflow, high efficiency and liquidity (this could be a pro or con depending on how you look at it), lack of significant leverage, etc.
Out of all those things however, we’re gonna focus on two of them. The lack of cashflow and the lack of leverage. Both of these things are abundant in real estate in particular. A good rental multifamily can be expected to have a cap rate of 7-12% with a cash on cash return ideally around 15% or higher. This is because 1: real estate does not rely upon appreciation solely, it relies upon the income it generates from the renters and 2: investment properties typically only need a 20% down payment in order to purchase.
That’s a 5:1 leverage ratio which would be impossible to achieve safely in the stock market.
Now it used to be that stocks had lower appreciation and higher dividend yields, however that has not been the case for 70 years at least.
You can take a look at this dividend yield chart of the S&P 500 for reference.
Luckily, We Can Turn The Stock Market Back Into An Income Machine Using Options
This is the whole premise of the theta-gang position. We replace our stock appreciation with premiums received from selling options as a sort of “dividend yield.”
So we turn to selling puts and calls on SPX or SPY or whatever index you prefer (unless you decide to sell puts and calls on individual companies within the indexes like me). That’s great, but if we compare it to real estate, we’re still missing the essential component of leverage.
That’s where leveraged ETFs come in.
Last article we explained the benefits of using them for long term growth, but what about for income generation by selling options on them?
Surely that should work right?
Well it should… if we do it correctly.
We mentioned before that leveraged ETFs suffer from something called “volatility decay,” basically just describing the idea that a when a loss is incurred, a greater gain needs to be made to square ourselves back to zero. With leverage we magnify our risk to this factor.
So because we have more vulnerability to downside, let’s protect ourselves using a bit of probability.
Using Standard Deviation To Calculate Probabilities
Let’s just assume for the moment that all market movements are as good as being random. Yes, they are based on data, but if we don’t have access to said data, the movements may as well be random.
Under this assumption we can then also assume that there are probabilities to which direction a stock is going to move. There should be roughly a 50% chance that the stock will go up or down at any given moment.
On top of that, we could also assume that larger movements are less likely than smaller movements, mainly due to the fact that it takes much larger sudden inflows and outflows of cash to make a stock behave that way. Now some stocks have a “relatively” higher ability to make a significant move in either direction, but even these stocks still have boundaries where they will be unlikely to move.
A good example of this how wild Tesla’s swings are relative to General Electric. Tesla has a higher relative swing compared to General Electric, but even Tesla is unlikely to swing to $30 or $5000 in the next year.
Now these observations we just made are the fundamental ideas behind the concept of “standard deviation.”
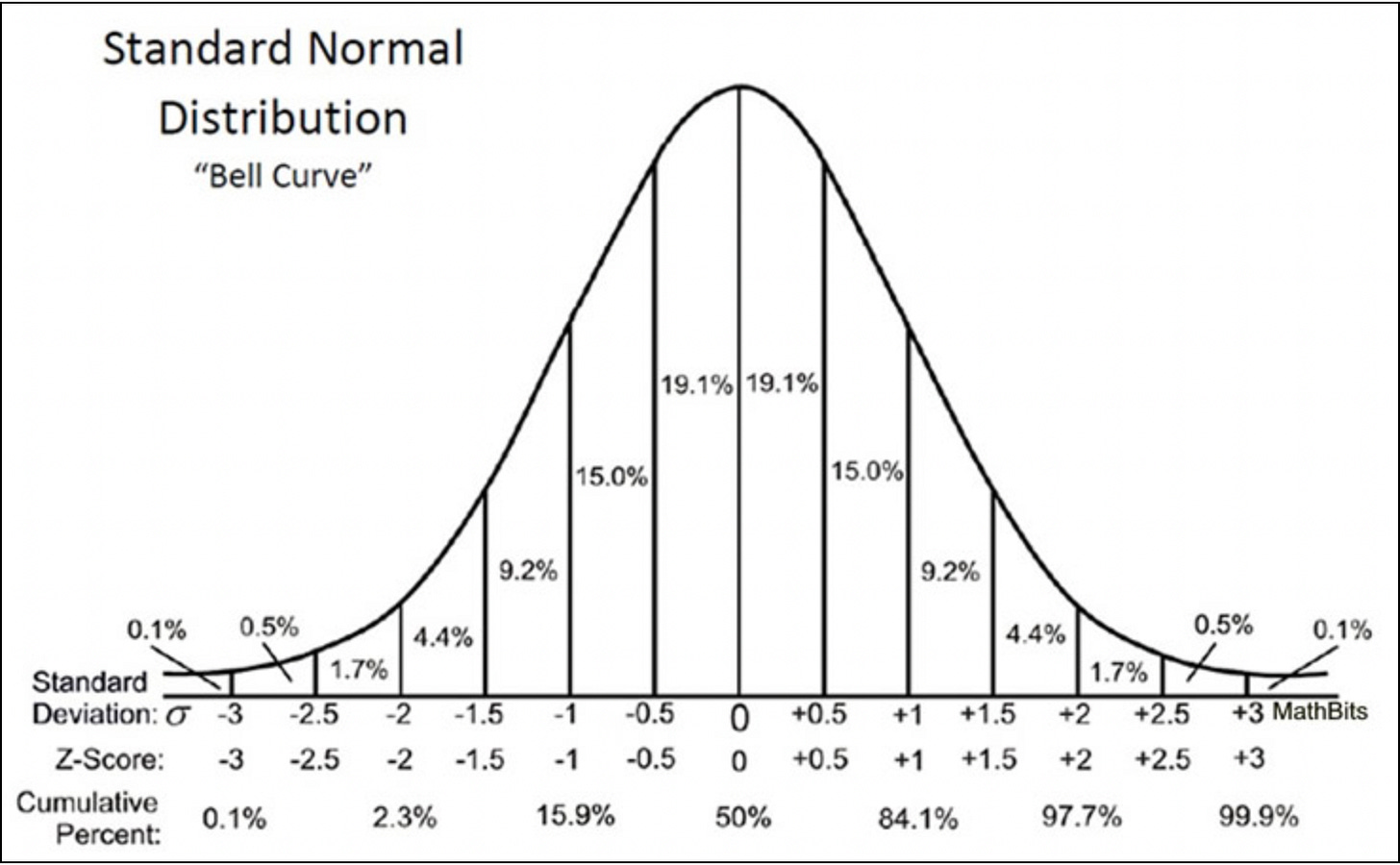
Standard deviation essentially says that within a given time frame (usually a year) a stock has a certain probability of being within certain price ranges based on its volatility (its ability to make wild swings like Tesla).
As you can see at the bottom of the chart we see that at each increasing or decreasing standard deviation (0.5, 1, 1.5, 2, 2.5, etc) there is less of a probability that our data (or in this case the stock price) will fall into this range given a “normal distribution.”
If you add up all the percentages between -1 and 1 we get a 68.2% chance that our stock price will fall in this range. This is called the first standard deviation. If we expand out the -2 and 2 then we get a 95.4% chance that our stock price will fall within the range. That is called the second standard deviation. If we go out to the 3 on each side we get a 98.8% chance that the stock price will fall within the range. With each standard deviation the chance that a stock price will fall within the range gets higher, albeit at a much slower rate.
So What Does This Have To Do With Selling Options?
Using these standard deviations we can get probabilities that a stock will fall within a certain range. If we use something called Implied Volatility we can figure out what the market thinks that one standard deviation is. Then using that, we can predict what probability our option has of expiring in the money (which is what we don’t want).
To find implied volatility we can go to a website like volafy.net and get the implied volatility percentage. In the case of TQQQ (QQQ leveraged 3x) the implied volatility is 78.97% at this time of writing.
Using this percentage we can plug it into a handy formula to calculate the standard deviation for any specific option.
The formula looks like this:
(sqrt(option days until expiration/365)) * implied volatility * current stock price
In written terms basically we divide the days until expiration by 365, then take the square root of that and multiply it by the implied volatility percentage and the current stock price.
That gives us the amount in dollars of the first standard deviation. If you take that amount and add it AND subtract it from the current price it will give you the range the stock will fall within 68% of the time.
Right now we are interested in selling puts on TQQQ without getting exercised, so we’ll sell at one standard deviation out of the money. At the current price of TQQQ ($57.02) the first standard deviation out of the money would be $46.22 (which is also 57.02 - 10.80).
If we go back up to our standard deviation chart we can see that on the left side of the chart (the side that represents our OTM options) we can add up all the percentages before the 1st standard deviation mark. This comes out to be a 15.9% that our OTM option will become ITM by expiration. If we are selling monthly options, this comes out to be getting assigned once out of every six months on average. To me, those seem like pretty good odds.
So let’s scroll down to the $46 strike put on TQQQ which is trading $105 per contract right now. That’s a 2.3% ROI in 21 days or 27.6% annually.
If we assume assignment twice a year that wipes out any premiums made for that given month we are still sitting on a 23% CAGR.
But Wait, Isn’t This Riskier Than Selling Puts On Regular Old QQQ?
This is the beauty of it, you have the same risk of getting assigned on TQQQ as you do with QQQ if you stay at the same standard deviation, but still receive 3x the premium. This is because with TQQQ higher volatility we sell further OTM than we would with regular QQQ but still receive the high premiums due to it being a leveraged product.
Anyway, if you have any thoughts on this, please drop them in the comments below!
If you found this post helpful we would appreciate it if you would take a moment to share it. We’ll make it easy with this big green button.
Until Next Time!
Disclaimer:
All content is for discussion, entertainment, and illustrative purposes only and should not be construed as professional financial advice, solicitation, or recommendation to buy or sell any securities, notwithstanding anything stated.
There are risks associated with investing in securities. Loss of principal is possible. Some high-risk investments may use leverage, which could accentuate losses. Foreign investing involves special risks, including a greater volatility and political, economic and currency risks and differences in accounting methods. Past performance is not a predictor of future investment performance.
Should you need such advice, consult a licensed financial advisor, legal advisor, or tax advisor.
All views expressed are personal opinion and are subject to change without responsibility to update views. No guarantee is given regarding the accuracy of information on this post